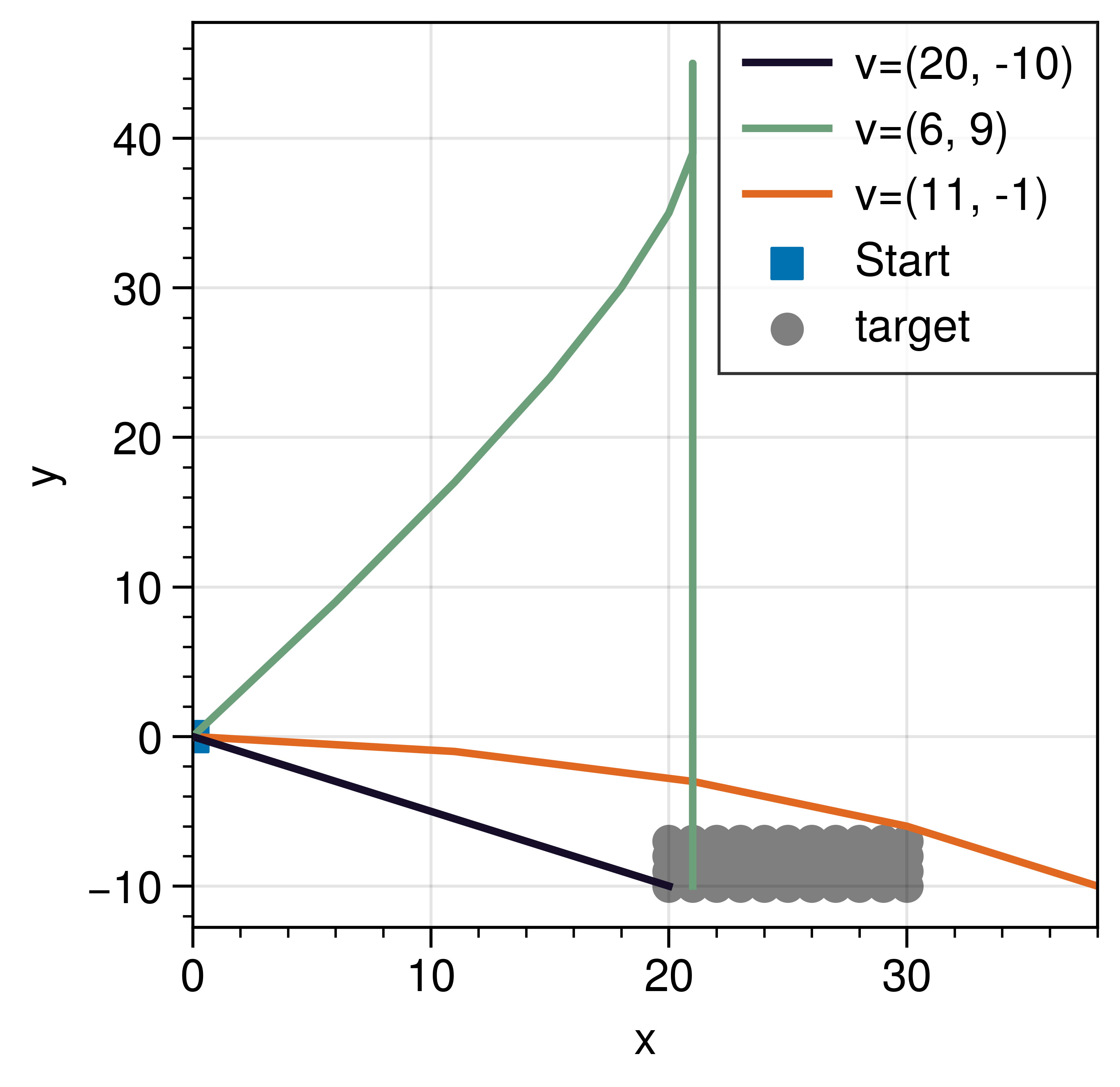
Table of Contents

1. Introduction
2. The problem
3. Step 1: Reaching the target area.
4. Step 2: Determining the max height
5. Finding the trajectory with the max height.
6. Reflections and conclusions

Introduction

Over the years I have grown quite fond of solving riddles. There is something thrilling about reasoning through a problem and finding non-trivial properties about seemingly trivial things. To me programming gives a similar experience; by using the tools of a programming language words are strung together to provide sentences that can be used to solve a real-world problem like finding the most efficient route between A or B, find the minimum state of a system moving over an energy landscape, sort files in a folder using a particular regex and so on.

Without knowing it, my interest for riddles was hidden in programming. Programming to me was a tool to reason through complex logical problems. Programming allowed me to verbalize the complex logical problem. This verbalization is very important. A few years ago, I attended a book reading from an author who expressed that speaking a language also invokes a form of thinking, and by speaking a different language your thinking would also be bend and used in a different way. After programming many years in python, and matlab. I have gotten a little bored of the way python speaks. I wanted to think differently.

Then last christmas, I read a blog that used the advent of code to learn a new programming language. The advent of code is an initiative that poses different programming exercises of increasing difficulty. The idea sparked interest in me and I set out some months ago to satisfy my need to learn a new language and attempt to solve some difficult riddles.

The advent code is an initiative that started in 2015. It starts 25 days before christmas with a new programming exercise every day leading up to christmas. The difficulty of the problem increases as the christmas approaches.

In this particular post, I will focus on day 17 of the advent of code 2021 as it beat my but and it need not have to!

The problem

The theme of the advent of code 2021 is helping Santa’s elves finding a key that was dropped in the ocean. On day 17, you are trying to shoot a probe from you submarine such that it hits a particular area (see figure below). The probe is shot with a velocity in the x, and y-direction. Each simulation step, the x, and y-velocity decreased by 1 where the x-velocity has a minimum of 0 and y-velocity can grow to -infinity. The aim is to find a trajectory that hits the target and for which the y-position is maximized. Seems easy right?

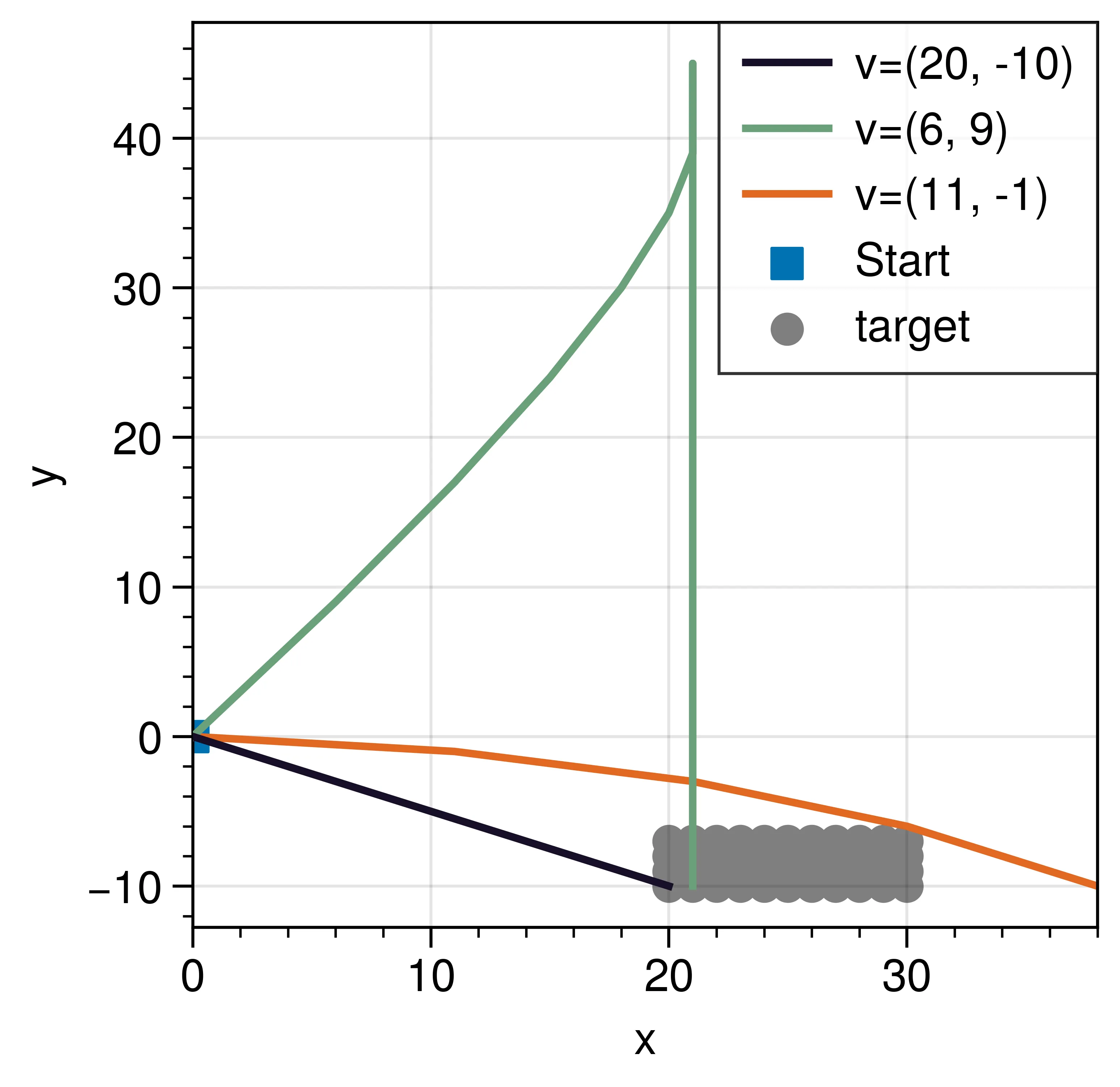
What ended up being difficult is that it is not trivial to determine the final position of the probe given an initial velocity. Let’s say that the probe has velocity. The position of the probe at timeis determined as

In the continuous case, any trajectory which intersects with the target will be a valid trajectory. However, in the discrete scenario, the probe may overshoot the target. That is, there may be a gap which for which betweenandthe probe misses the target. I decomposed the problem in two steps. First, we need to figure what properties the trajectories that hit the target have. Second, we focus on finding the trajectory that maximizes the height of the trajectory.

Step 1: Reaching the target area.

Initially I had the intuition of plotting the dynamics of the of the velocity over time. The distance traveled in the x-direction takes the form of a sum of integers. Luckily, for the sum of integers there is a nice expression: the Gauss sum which takes the form

To see why this is, write down a sequence of positive integers, e.g.. Next, take pairs form the outside in and notice how the sum of these pairs are equal. For example, the sum ofis equal to the sum of(by moving “inwards”). Since we haveof these pairs Gauss deduced a nice closed-formed solution for the sum. This property is pretty nifty to use in the computation of the distance, as it prevents a possible large sum in determining the distant traveled. Our distance computation therefore becomes

In order to hit the target, we need to compute the bounds which are allowed forand. Let’s consider thedirection first as it is slightly easier to understand. The maximumthat is allowed is the velocity in which afterstep, thedistance travels still hits the target. This is true forwhereof the target is the right most limit of the target. The minimum velocity forcan be found by considering that for somethe sum of the velocity will need to reach the left limit of the target. The distance moved alongdirection is capped of when. This point is reached whenis decreased to zero or distance traveled along thedirection is

The-direction is a bit more challenging to compute as the distance traveled does not have a cap like thedistance has. Yet, we can still deduce some bounds. Similar to thedirection, the max velocity inis capped by the distance traveled instep. That is, the fasted you can reach the target, is by throwing the projectile with. For the minimum-velocity, we note the following: aftertime steps, the trajectory reaches its apex, and afterthe trajectory reaches the line. The minimumvelocity has to match the maximum distance fromto the target. That is, forthe velocity. In other words, relative to the line, the velocity has to match at most. This gives us the bounds

Side note: some other random property I found was that when you have some velocityand it is shifted by 1, the followingdistance also shifts by 1. That is,for the same time-span.

Step 2: Determining the max height

For a given starting velocitythe max height will be reached whenreaches zero. This is readily computed using the Gauss sum:

For example forthe max height will be zero, and forthe max height will be 6.

Finding the trajectory with the max height.

Finding the highest trajectory now merely involves evaluating the over the ranges indicated in step 1 and keeping track of the starting velocities that yield the highest value (step 2). A “priority queue” can be used to quickly find the max value: by starting from strongestvelocities first, the first trajectory that lands within the target area, will also be the starting velocity that maximizes the height.

Reflections and conclusions

Initially, I approached this problem by looking at the various ranges that the velocities inandcan take. I spent quite some time thinking of a clever way to somehow come up with a closed-form solution. Since I was writing the code up in Nim I did not have access to fancy optimization libraries found in for example python (or at least I didn’t look for one). This prompted me to look further than merely over complicated the problem and throwing some fancy abstract analysis on it. After a couple of hours, the problem seemed easier when looking at it from the right perspective. Here, the trick was realize that the optimization had to involve identifying the correct ranges and setting up a priority queue. Overlooking these ranges gives no guarantees if the solution converges although brute-force approaches will give you the proper solution.

After nearly 17 exercises in Nim, my experience with coding up examples and structuring code improved remarkable. When the time is ripe I will post a full solution and reflection on my adventure with advent and Nim in a future post. For now, I would like to remark that taking up this task was initially not easy. Implementing simple ideas takes more time, and nearly everything has to be looked up. Looking back, the ease at which I write Nim code is faster and more fluent than the initial couple of exercises. I also appreciate how free Nim is in expressing your thoughts; functions operate on data and the way your write these operations are rather free.

The speed of programming in a novel language shows both a maturating of the knowledge I have acquired of programming languages I can fluently write, but also a manner of thinking. Techniques and algorithms that are relatively easy in language A becomes more challenging or impossible in language B; one has to look for other approaches to harness the power of that particular language. Nim is a powerful language that writes really well. It’s too bad that is does not score higher among the programming popularity charts.

As the months progress and christmas seems like a vague memory, I feel the pressure of finishing these programming riddles. There is a remarkable difference in difficulty for the earlier exercises and the latter ones. For some exercises, I found multiple solutions. I believe this one also has a nice mathematical solution that seems to escape me and I may come back to it later and update this post. To me, these exercises form a nice brain tease and I will slowly work through them when I find the time. See you in the next post!