· Philosophy · 10 min read
Rocks, minds, and Turing machines
What does it mean to compute?
Central to my work is the process of taking ideas and turning them into programs that can be executed by a computer. This process is often referred to as “computation.” The models I construct are meant to provide an understanding of the natural world by encoding causal rules inside a model, which can then be implemented by manipulating bits in a computer. In essence, we equate the operations in a computer at an abstract level with operations in the real world. This has interesting consequences. For example, if we simulate a rock falling inside a computer, can we claim that the real-life rock also computes its trajectory when it falls? If so, does that mean that everything in the universe is computing all the time?
This thought occurred to me many moons ago and prompts me now to get a bit more precise about what computation is, and what this means for our understanding of the world.
What is computation?
Consider the following statements:
My intuition says the first example is a case of computation. It provides an input (the numbers 1, 2, and 3), an operation (addition), and an output (the number 6). The second example, however, is more ambiguous. It represents an equation that can be solved, but it does not provide a clear input-output relationship in the same way as the first example. One could argue that the process of solving the equation is a form of computation, but the equation itself is not computation in the same sense.
In general, computation can be defined as the process of taking an input, applying a set of rules or operations to that input, and producing an output. Does this entail, then, that a rock falling through the pull of gravity is computing its trajectory? After all, the rock has an initial position and velocity (input), is subject to the laws of physics (rules/operations), and follows a specific path (output).
The definition of what can compute, therefore, can be stretched to mean different things. We could refer to natural systems as those created by the forces of evolution, artificial systems such as computers, or abstract systems such as mathematical constructs.
The use of these different ideas has led to a wide variety of perspectives surrounding the nature of computation. Below, I outline a few of these ideas.
Views on computation
Following our intuition above, we can see that computation is not a straightforward concept. It has something to do with the ability to define different parts of the process. In particular, we need to be able to define the inputs, the outputs, and the potential operators over them.
The brain and computation
One of the most natural ways to think about computation is to wonder if we humans compute. Are our thoughts a reflection of some computational process? If so, what does that mean for the world around us? Can we say that the world itself is computing?
Jerry Fodor’s work in cognitive science offers a compelling view of computation as the foundation of human thought. According to his “Language of Thought” hypothesis, mental processes are computational in nature, operating over a symbolic system akin to a language. This perspective aligns with the idea that computation involves the manipulation of symbols according to formal rules. For Fodor, the mind itself is a kind of computational system, where inputs (sensory data) are processed through rules (mental algorithms) to produce outputs (thoughts or actions).
Fodor draws a crucial distinction between syntax, the formal rules by which computations occur, and semantics, the meaning behind those symbols. This distinction sets human cognition apart from artificial computing systems, which often manipulate symbols without any inherent understanding of their meaning.
Take, for example, the concept of an “apple.” In a computer, an apple might be represented as a series of characters, which are themselves encoded as a sequence of binary bits—ones and zeros, or on/off currents in transistors. For the computer, these bits could just as easily represent a whale, a number, or any other arbitrary concept. The meaning of “apple” only emerges when a human assigns that specific interpretation to the bits stored in memory.
In contrast, the human experience of an apple is deeply tied to its meaning. An apple is not just a symbol; it is connected to sensory experiences (its taste, texture, and smell), actions (eating or picking it), and even cultural or personal associations (e.g., the apple falling on Newton’s head). This rich semantic context is what gives the concept of an apple its meaning for humans.
Fodor’s view highlights that human cognition is fundamentally computational, but it is a computation deeply intertwined with meaning. This stands in stark contrast to artificial systems, which, while capable of processing symbols with incredible speed and precision, lack the semantic depth that characterizes human thought.
Beyond the mind: universality of computation
The distinction between semantics and syntax is important because it allows us to study the two separately. One could argue that Fodor’s view is too limited, as semantics can be seen as an emergent property of human experience and its interaction with the environment.
Hilary Putnam extends the boundaries of computation by suggesting that it is not tied to any specific physical medium. His theory of functionalism posits that mental states are computational states, meaning that any system capable of performing the same computations could, in principle, exhibit the same mental states. This idea opens the door to interpreting natural phenomena as computational processes. For example, the trajectory of a falling rock could be seen as a computation if we describe its initial position and velocity as inputs, the laws of physics as rules, and its path as the output. Putnam’s work challenges us to consider whether computation is a universal property of systems, whether natural, artificial, or abstract.
Alan Turing: The Foundations of Computation
Alan Turing’s contributions provide the formal backbone for understanding computation, especially through his concept of the Turing machine. This model defines computation as a process involving inputs, a set of rules, and outputs—a framework that is not only the foundation of modern computer science but also a lens through which we can examine the computational nature of the universe.
The Turing machine perfectly illustrates the mechanistic or algorithmic view of computation. In this perspective, computation is the manipulation of objects—usually symbols—by following precise, deterministic rules. Imagine a machine with an infinite tape (serving as memory), a read/write head that moves along the tape, and a table of instructions that tells the machine what to do at each step. The process is entirely mechanical: given an initial state and some input, the machine transforms the tape step by step, each operation repeatable and rule-based. This approach shows that any algorithmic process—no matter how complex—can be broken down into simple, mechanical steps.
The Turing machine provides a bridge between the abstract world of mathematical operations and their physical realization in devices. For example, we can model the trajectory of a falling rock using mathematical equations, and then implement these equations as algorithms on a Turing machine—effectively making the abstract model “physical” through computation.
However, this connection is not always perfectly reversible. While any algorithm executed by a Turing machine can be described mathematically, not every physical process or device necessarily corresponds to a well-defined mathematical equation or computation. In other words, computation allows us to instantiate abstract models in the physical world, but not every physical system is guaranteed to be representable as a computation in the Turing sense.
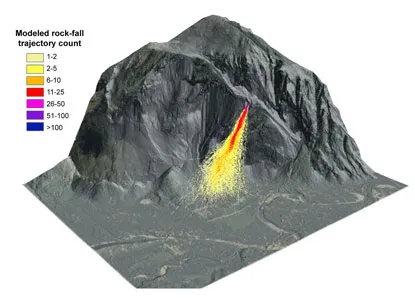
For the mapping to work in reverse, we must be able to clearly identify and formalize the rules that govern the system’s dynamics. This becomes especially challenging with complex adaptive systems, where the underlying rules or mechanisms may be ambiguous or emergent. Consider, for example, starling murmurations: the mesmerizing flocking behavior of these birds at dusk appears to emerge from simple interactions, yet the precise rules and the full richness of the phenomenon are difficult to capture mathematically (and perhaps even nonsensical to formalize). While agent-based models can emulate flocking with a handful of simple rules, the actual observation and quantification of such emergent behavior in nature is much harder to formalize—and thus, harder to encode as a computation in the Turing sense.


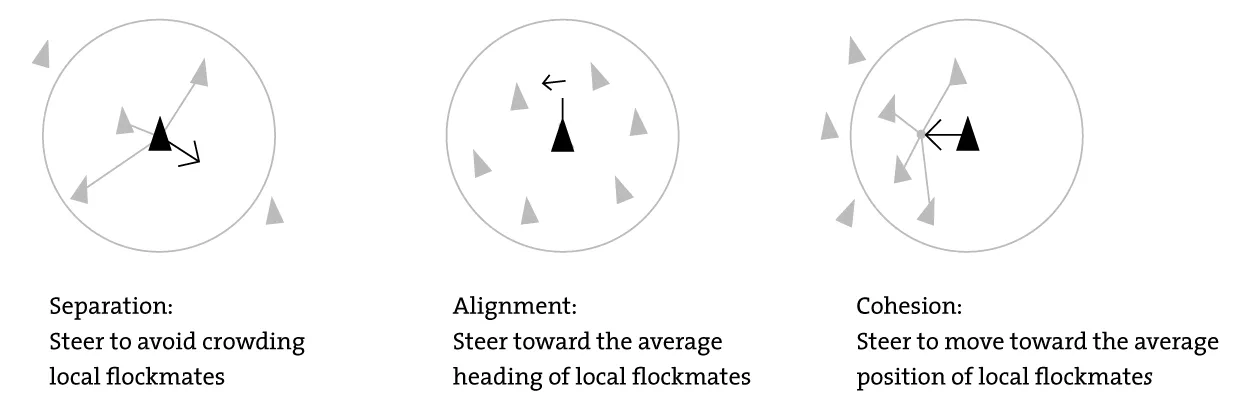
Panels A–C: A) Starling murmurations at dusk exhibit emergent, fluid-like collective motion (source). B) From observation to simple local rules in a boids-style simulation (source). C) The three canonical Boids rules—separation, alignment, and cohesion (source).
These challenges highlight a deeper question: what kinds of systems truly compute, and how far can we stretch the concept of computation? The difficulty in formalizing emergent or complex behaviors suggests that computation may not be a universal property, but rather one that depends on our ability to clearly define inputs, rules, and outputs.
Computation Across Natural, Artificial, and Abstract Systems
The perspectives of Fodor, Putnam, and Turing converge on a fascinating point: computation is not confined to machines or human minds. Natural systems, such as the trajectory of a falling rock, artificial systems like computers, and abstract systems such as mathematical constructs, all challenge our understanding of computation. For instance, when we simulate a rock’s fall inside a computer, we are encoding the causal rules of the natural world into a model. But does this mean the rock itself is computing its trajectory in real life? Or is computation something unique to systems that manipulate symbols or follow explicit algorithms?
This question becomes even more intriguing when we consider abstract systems. A mathematical equation, for example, represents a set of relationships that can be solved computationally. But is the equation itself a computation, or is it merely a framework for computation to occur? The ambiguity here mirrors the broader challenge of defining computation in a way that encompasses its diverse manifestations.
Toward a Broader Understanding of Computation
“Does a rock compute?” is the wrong question. The right one is: under which representation does a rock’s motion become a computation?
If we reserve “computation” for cases where inputs, rules, and outputs are well-specified, two things follow. First, simulation becomes a disciplined way to test causal stories about the world: we fix a representation, encode the rules, and see whether the outputs match observations. Second, limits matter. In systems with emergence and adaptation, the very choice of representation can make state transitions legible—or hide them. When we cannot stably identify inputs or rules, calling the system “computational” carries little explanatory value.
This is a pragmatic stance with a provocation built in. Computation is not whatever the world does; it is a contract between a model and a system, negotiated through representation. Under one contract, a falling rock computes its next state; under another, a murmuration resists being cast as an algorithm. Pushing that boundary clarifies where our models grip reality and where they slip.
The work ahead is to choose representations that make dynamics computable enough to explain and to act—without pretending everything is. In upcoming work, I’ll turn to symbol grounding and semantics: when, and how, computations become “about” the world rather than just manipulations of symbols.